Sometimes you may need to correct power factor (PF) at a single motor. This means sizing PF capacitors for that motor. The good news: If you size these capacitors correctly, you'll lower your electrical energy usage costs. The bad news: If you size them too small, you may not accomplish much. The worst news: If you size the capacitors too large, the PF vector swings way past perpendicular, leaving you in a very unfavorable situation. But don't worry, calculations to get the proper kVAR value and correct PF capacitor size are straightforward.
Sizing the capacitor
First, you need to collect the full-load PF and efficiency information on the motor in question. You can often get this directly from your motor supplier in the form of product data sheets, CD-ROMS, or right off its Web site. It wouldn't hurt to check the motor manufacturer's Web site either.
Second, you need your motor's input rating in kW. To get that, you'll probably need to do some simple conversions, which start with very simple calculations as shown in Equations to Know. Basically, you'll need to determine the input kW, as shown in Equation 2.
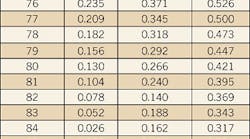
Now that you have this number, you can refer to a PF correction table (Table 1). Looking at the Table, go in from the left with the existing PF, and then come down from the top with the desired PF. Where the two lines intersect, you'll find the multiplier you need. Take that multiplier and multiply the motor's input kW by it. This will give you the required kVAR of correction.
Finally, using the data in Table 2, select a capacitor, rounding down to the next lower value. You now have the correct size capacitor for your PF correction plan. For a typical installation, see Calculation Procedure Example.
A typical way of installing a capacitor in this type of application is to connect it between the starter and the single motor. This connection reduces the current flowing through the starter and overload relay.
Resizing the overload heaters
Now let's think about the overload heaters. You've installed them in the starter, right? And you sized them according to the current the starter will see, based on the motor load. If you reduce the amount of current through the starter, the existing heaters won't be able to protect the motor. So, you have to reduce the heater size to accommodate the reduced current through the starter, or you'll be running an under-protected motor.
The motor itself will draw the same magnitude of current at full load as it would without PF correction. However, the PF capacitor will supply a portion of the current to the motor. Only the balance will come through the starter from the power line. You can determine the new value of current passing through the overloads by using Equation 3.
If you were going to do this for the motor in our previous example, the math would look like that shown in Heater Current Calculation Example.
Rules of caution
When correcting PF at a single motor, follow these guidelines:
Rule 1: Don't get overly corrective with your PF correction. You should target the PF correction for the motor's running current, not its starting or full load current. In other words, always under correct; the cost is a slight loss of PF. If you over correct, the costs pile up because of high transient torques, overvoltages, and other problems you need to avoid. You should consider 95% correction as the upper limit, with 90% being the optimum target.
Rule 2: Never use this type of PF correction with a motor that's controlled with a solid-state device, such as a soft-start or variable-frequency drive. If you do have a PF problem and are using such a device, you should contact the device manufacturer for a solution. The manufacturer's expertise and exposure to thousands of users can save you time, money, and downtime. The manufacturer will be more than happy to help you.
Sidebar: Equations to Know
Equation 1: Converting motor horsepower to kW of motor output
kWMOTOR OUTPUT = hp × 0.746
Equation 2: Converting output kW to input kW
kWMOTOR INPUT = kWMOTOR OUTPUT ÷ (% Efficiency ÷ 100)
Equation 3: Converting uncorrected current to corrected current
ISTARTER CORRECTED = IMOTOR FLA × (PFORIGINAL ÷ PFCORRECTED)
Sidebar: Calculation Procedure Example
What is the kVAR of a PF correction capacitor needed to improve the PF of a 100-hp motor to 95% at full load?
Step 1: Look up the existing PF and efficiency
In our case, the existing PF is 85%, and the motor is 94.7% efficient.
Step 2: Convert the hp to kWOUTPUT
Using Equation 1, we get:
kWMOTOR OUTPUT = hp × 0.746 = 100 × 0.746 = 74.6kW
Step 3: Convert output kW to input kW
Using Equation 2, we get:
kWMOTOR INPUT = kWMOTOR OUTPUT ÷ (% Efficiency ÷ 100) = 74.6kW ÷ 0.947 = 78.8kW
Step 4: Find multiplier to get desired PF correction
In our case, we want to correct the PF from 85% to 95%. Looking at Table 1 and going down the 95% column and across the 85% column, we see that the intersection is at 0.291, which is the multiplier we need.
Step 5: Multiply input kW by multiplier
The calculation is 78.8 × 0.291 = 22.9 kVAR.
Step 6: Select closest kVAR value
Using Table 2, we see that closest value rounded down is 22.5 kVAR.
Sidebar: Heater Current Calculation Example
Using the same 100-hp motor as in the Calculation Procedure Example, you would normally select a heater size based on a current of 118A. However, when you use Equation 3 to correct for PF, you have to select a heater size based on a new number.
Here's how you arrive at that number:
ISTARTER CORRECTED = IMOTOR FLA × (PFORIGINAL ÷ PFCORRECTED) = 118 × (0.85 ÷ 0.95) = 105.6A