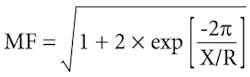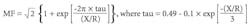This is the first of a two-part series on the processes used to find the short circuit current duties of circuit breakers and fuses. In Part 1, we’ll use a simplified power system to illustrate the methodologies for medium-voltage circuit breakers and fuses. In Part 2, we’ll do the same for low-voltage circuit breakers and fuses.
It’s important to note that this discussion is intended only to illustrate (by way of example) the ANSI methodologies to find the short circuit current duties to select the short circuit withstand and interrupting capabilities of ANSI-rated circuit breakers and fuses. Other ratings and application considerations beyond the scope of these two articles must be considered for the proper selection of circuit breakers and fuses. The reader is directed to the latest editions of the applicable ANSI/IEEE C37 standards, cited in the references of Chapter 10 of the IEEE Violet Book (IEEE Std 551-2006), for complete coverage.
Background
A short circuit fault is an unintentional phase-to-phase or phase-to-ground connection in an electrical system that is caused by insulation breakdown, equipment malfunction, or human error. Oftentimes, the short circuit fault causes an extremely high level of current to flow; and (1) electrical equipment must be capable of withstanding the extreme mechanical and thermal stresses associated with the short circuit current, and (2) interrupting devices must be capable of quickly and safely interrupting the short circuit current. Inadequate short circuit withstand or interrupting capability can lead to catastrophic failure of equipment, posing a threat to facility operations (i.e., electrical outage, infrastructure damage, or fire) and personnel (i.e., electric shock, burns, physical trauma, or death).
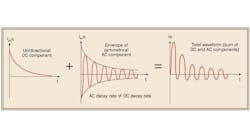
Figure 1 (above) illustrates a typical short circuit current waveform for one phase of a 3-phase synchronous generator, previously unloaded, which has been subjected to a bolted 3-phase short circuit across its accessible terminals. The asymmetrical short circuit current waveform can be broken down into two components: 1) a unidirectional (DC) component; and 2) a symmetrical alternating (AC) component. The DC component exponentially decays to zero, while the envelope of the symmetrical AC component eventually decays to a constant amplitude sine wave in the steady-state. The rate of exponential decay (or time constant) of the DC component is related to the short circuit X/R ratio, where X and R are the equivalent reactance and resistance at the fault location, respectively. To simplify analysis, steady-state AC circuit theory is exploited to calculate a worst-case (initial) root-mean-square (rms) magnitude of the symmetrical AC component to characterize a particular time interval of the fault-on time period. To simplify verbiage, the expression “worst-case (initial) root-mean-square (rms) magnitude of the symmetrical AC component” is hereafter shortened to “symmetrical rms current.”
Three types of networks are used to represent the power system over three time intervals of the fault-on time period. The first-cycle (momentary) network characterizes the first few cycles (at 60 Hz) of the fault-on time period. For this network, the AC motors and generators are modeled by first-cycle or subtransient reactances, and steady-state AC circuit analysis is used to calculate the first-cycle (momentary) symmetrical rms current. To account for the DC component of the short circuit current waveform, the first-cycle (momentary) symmetrical rms current is multiplied by an appropriate multiplying factor (MF) to yield the first-cycle (momentary) short circuit current duty; and first-cycle (momentary) short circuit duties must not exceed: (i) closing and latching (momentary) capabilities of medium-voltage circuit breakers, (ii) interrupting capabilities of medium-voltage fuses, (iii) interrupting capabilities of low-voltage circuit breakers, and (iv) interrupting capabilities of low-voltage fuses. The contact-parting (interrupting) network is used to calculate the contact-parting (interrupting) symmetrical rms current for medium-voltage circuit breaker minimum contact-parting times of 1.5 to 4 cycles after the inception of the short circuit fault. For this network, the AC motors and generators are represented by different (same or larger) constant reactances than those for the first-cycle (momentary) network. To account for the DC component of the short circuit current waveform, the contact-parting (interrupting) symmetrical rms current is multiplied by an appropriate MF to yield the contact-parting (interrupting) short circuit current duty; and contact-parting (interrupting) short circuit current duties must not exceed the interrupting capabilities of medium-voltage circuit breakers. Finally, the approximately 30 cycle network is a minimum source representation that characterizes the faulted power system in the steady-state (beyond 30 cycles), and it is used to investigate whether minimum short circuit currents are sufficient to operate current-actuated relays.
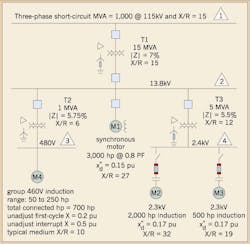
Fig. 2. One-line diagram of simplified industrial power system.
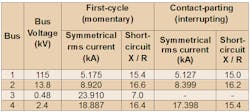
Figure 2 (above) is a one-line diagram of a simplified industrial power system we’ll use to illustrate the ANSI methodologies to find the short circuit current duties of ANSI- rated medium-voltage circuit breakers and fuses. The Table below summarizes the results of the short circuit study by listing the first-cycle (momentary) and contact-parting (interrupting) symmetrical rms currents and short circuit X/R ratios for a bolted 3-phase fault at each bus. [In general, it is important that the study be performed on the system configuration involving maximum fault current contributions. The reader is directed to Chapter 9 of the IEEE Violet Book (IEEE Std 551-2006) and the references cited therein for the procedure to perform these calculations.] Note in the Table that the contact-parting (interrupting) symmetrical rms current and short circuit X/R ratio are not listed for low-voltage Bus 3, since the interrupting capabilities of low-voltage circuit breakers and fuses are selected based on first-cycle (momentary) short circuit current duty. As mentioned earlier, we’ll discuss the methodologies to find the short circuit current duties of low-voltage circuit breakers and fuses in Part 2.
Finally, it should be mentioned that the bolted 3-phase fault represents the worst-case condition at every bus of this example, insofar as contact-parting (interrupting) short circuit current duty is concerned. Generally speaking, the bolted single line-to-ground fault could represent the worst-case condition, and the methodologies to calculate contact-parting (interrupting) duty will differ from those described below. [For an example of this case, the reader is directed to Sec. 5.3 of ANSI/IEEE C37.010-1979 for the older constant MVA rated medium-voltage circuit breakers and Sec. 6.3 of IEEE Std C37.010-1999 (R2005) for the newer constant kA rated medium-voltage circuit breakers.]
Medium-Voltage Circuit Breakers
Generally speaking, the appropriate MF to account for the DC component of the short circuit current waveform depends on the short circuit X/R ratio at the fault location and the rating structure of the interrupting device. Complicating the selection of the appropriate MF for medium-voltage circuit breakers is the fact that there is a huge installed base of medium-voltage circuit breakers whose short circuit ratings are based on older standards that differ significantly from the latest standards. Specifically, the historic constant MVA rating structure pre-dates the latest constant kA rating structure that was initiated around 1999. [See Siemens TechTopics Nos. 4 and 23 (available at www.energy.siemens.com/us/en/services/power-transmission-distribution/tech-topics-application-notes.htm) for a well-written summary of these rating structures.] Consequently, the procedures summarized below to select the appropriate MFs to calculate the short circuit current duties of medium-voltage circuit breakers are classified according to rating structure. [The reader is directed to Chapters 9 and 10 of the IEEE Violet Book (IEEE Std 551-2006) for detailed coverage of these procedures.]
First-Cycle Duty (Constant MVA Rated Breakers)
First-cycle (momentary) duty of Bus 2 medium-voltage breakers = MF × Bus 2 first-cycle (momentary) symmetrical rms current = 1.6 × 8.920kA = 14.272kA (asymmetrical rms)
The closing and latching (momentary) withstand capabilities of constant MVA rated medium-voltage circuit breakers in rms kA must exceed the first-cycle duty in asymmetrical rms kA.
Note: MF = 1.6 is applicable whenever the first-cycle short circuit X/R ratio is less than or equal to 25. If the first-cycle short circuit X/R ratio exceeds 25, the following formula can be used to calculate the MF.
First-Cycle Duty (Constant kA Rated Breakers):
The closing and latching (momentary) withstand capabilities of constant kA rated medium-voltage circuit breakers in peak kA must exceed the first-cycle duty in asymmetrical peak kA.
First-cycle (momentary) duty of Bus 2 medium-voltage breakers = MF × Bus 2 first-cycle (momentary) symmetrical rms current = 2.6 × 8.920kA = 23.192kA (asymmetrical peak)
Note: MF = 2.6 is applicable whenever the first-cycle short circuit X/R ratio is less than or equal to 17. If the first-cycle short circuit X/R ratio exceeds 17, the following formula can be used to calculate the MF.
Interrupting Duty (Simplified Method)
The simplified method to find the contact-parting (interrupting) short circuit current duty applies to constant MVA or constant kA rated medium-voltage circuit breakers and uses a conservative MF of 1.25, rather than calculating the MF from a formula based on the contact-parting short circuit X/R ratio.
Contact-parting (interrupting) duty of Bus 2 medium-voltage breakers = 1.25 × Bus 2 contact-parting (interrupting) symmetrical rms current = 1.25 × 8.399kA = 10.499kA (asymmetrical rms)
The required symmetrical interrupting capability of the medium-voltage circuit breaker in rms kA must exceed the contact-parting (interrupting) duty in asymmetrical rms kA, where the required symmetrical interrupting capability depends on the rating structure as follows.
Constant kA rated breakers: For operating voltage less than rated maximum design voltage, the required symmetrical interrupting capability = rated short circuit current, where the rated maximum design voltage and rated short circuit current are listed in the manufacturer’s table for constant kA rated medium-voltage circuit breakers.
Constant MVA rated breakers: For operating voltage between (1/K) × rated maximum design voltage and rated maximum design voltage, the required symmetrical interrupting capability = rated short circuit current × (rated maximum design voltage ÷ operating voltage).
For operating voltage less than (1/K) × rated maximum design voltage, the required symmetrical interrupting capability = K × rated short circuit current = maximum symmetrical interrupting capability, where voltage range factor K, rated maximum design voltage, rated short circuit current, and maximum symmetrical interrupting capability are listed in the manufacturer’s table for constant MVA rated medium-voltage circuit breakers.
Interrupting Duty (Only Remote Sources)
A less conservative method than the simplified method takes into account the actual decay of the DC component of the short circuit current waveform, but assumes no decay in the envelope of the symmetrical (AC) component. The assumption of no AC decay is characteristic of a power system without local (in-house) generation. Note the following procedures differ by rating structure. [For further details, the reader is directed to ANSI/IEEE C37.010-1979 for the older constant MVA rating structure and IEEE Std C37.010-1999 (R2005) for the newer constant kA rating structure.]
Constant MVA rated breakers: Contact-parting (interrupting) duty of Bus 2 medium-voltage breakers = MF × Bus 2 contact-parting (interrupting) symmetrical rms current = 1.0 × 8.399kA = 8.399kA (asymmetrical rms), where MF = 1.0 was found from the curve in Fig. 10 of ANSI/IEEE C37.010-1979 for a 5-cycle breaker with 3-cycle minimum contact-parting time and Bus 2 contact-parting (interrupting) short circuit X/R ratio of 16.2 from the Table. (Generally speaking, MF = 1.0 for a 5-cycle breaker with 3-cycle minimum contact-parting time if the contact-parting (interrupting) short circuit X/R ratio is 15 or less, because a certain degree of asymmetry is built into the rating structure.)
The required symmetrical interrupting capability of the medium-voltage circuit breaker in rms kA must exceed the contact-parting (interrupting) duty in asymmetrical rms kA. (The required symmetrical interrupting capability of constant MVA rated medium-voltage circuit breakers was described in the previous section.)
Constant kA rated breakers: Contact-parting (interrupting) duty of Bus 2 medium-voltage breakers = MF × Bus 2 contact-parting (interrupting) symmetrical rms current = 1.0 × 8.399kA = 8.399kA (asymmetrical rms), where MF = 1.0 was found from the curve of Fig. 10 of IEEE Std C37.010-1999 (R2005) for a 5-cycle breaker with 3-cycle minimum contact-parting time and bus 2 contact-parting (interrupting) short circuit X /R ratio of 16.2 from the Table. [Generally speaking, MF = 1.0 for a 5-cycle breaker with 3-cycle minimum contact-parting time if the contact-parting (interrupting) short circuit X/R ratio is 17 or less, because a certain degree of asymmetry is built into the rating structure.]
The required symmetrical interrupting capability of the medium-voltage circuit breaker in rms kA must exceed the contact-parting (interrupting) duty in asymmetrical rms kA. (The required symmetrical interrupting capability of constant kA rated medium-voltage circuit breakers was described in the previous section.)
Interrupting Duty (Local and Remote Sources)
The least conservative procedure to find the contact-parting (interrupting) short circuit current duty is applicable if the fault is fed by local and remote sources of short circuit current. Remote sources include the electric utility and those in-house synchronous machines that are electrically remote from the fault location. Local sources include those in-house synchronous machines that are electrically local to the fault location. [Induction motors local to the fault location may be classified as remote sources of short circuit current, because the AC decay effect in the induction motor short circuit current waveform has already been taken into account in the induction motor reactance multipliers for the contact-parting (interrupting) network. See Table 9-1 in the IEEE Violet Book (IEEE Std 551-2006) for details.]
The duty calculation makes use of both remote and local multiplying factors in a weighting process. The duty is calculated as the sum of the remote MF multiplied by the portion of the contact-parting (interrupting) symmetrical rms current from remote sources and the local MF multiplied by the remainder (local portion) of the contact-parting (interrupting) symmetrical rms current. [Another formula to calculate the duty, involving the so-called “no AC decay” ratio, yields an identical result. The reader is directed to Chapters 9 and 10 of the IEEE Violet Book (IEEE Std 551-2006) for details.]
Medium-Voltage Power Fuses
This discussion is limited to applications of medium-voltage power fuses for industrial and commercial power systems. The reader is directed to Chapter 6 of the IEEE Buff Book (IEEE Std 242-2001) for broader coverage of high-voltage power and distribution fuses.
E-rated power fuses are available as both expulsion and current-limiting types, while R-rated power fuses are available only as current-limiting type. E-rated current-limiting power fuses afford protection of power transformers, voltage (or potential) transformers, and capacitor banks; while R-rated power fuses afford short circuit protection in medium-voltage motor controllers. For symmetrical-current-rated power fuses, the first-cycle symmetrical rms current can be directly compared to the rated symmetrical interrupting capabilities in a manufacturer’s table only if the first-cycle short circuit X/R ratio at the fault point (i.e., source side of the power fuse) is 15 or less. In this context, “symmetrical-current-rated” implies that an MF to account for the DC component is unnecessary to adjust the first-cycle symmetrical rms current whenever the first-cycle short circuit X/R ratio is less than or equal to 15, because a certain degree of asymmetry is built into the rating structure. If the first-cycle short circuit X/R ratio exceeds 15, the manufacturer should be consulted for derating (reduction) of the published rated symmetrical interrupting capabilities. For the example at hand, the last statement applies, since the first-cycle short circuit X/R ratio for a 3-phase fault at Bus 4 is 16.4.
Mercede, P.E., is principal of Mercede Engineering LLC, based in Bryn Mawr, Pa. He can be reached at [email protected].