Variable current will generate inductance, capacitance, and their related properties of inductive and capacitive reactance. Although there's no energy loss that directly results from these properties, 90-degree out-of-phase voltage and current must be supplied so that the created magnetic and electric fields can be maintained. As a result, a small increase in conductor I2R loss will occur.
Of course, there are other reactances not related to conductors that make up a total system reactance, such as leakage reactances of apparatus and the extent of power factor control. We'll limit our discussion here to conductor reactance.
Inductive, capacitive reactance
This is the measure of an inductor's ability, in a fashion similar to that of a resistor, to oppose current. It's expressed by the following equation:
XL = 2ϖfL (Equation 1)
Where XL is inductive reactance (in ohms), f is frequency (in Hertz), and L is inductance (in Henries).
Note that inductive reactance is directly proportional to frequency. As frequency increases, inductive reactance also increases. You should be aware of the fact that inductive reactance causes current to lag voltage by 90 degrees.
Capacitive reactance is the measure of a capacitor's ability, in a similar fashion to that of a resistor or inductor, to also oppose current. It's expressed by the following equation:
XC = 1 ÷ (2ϖfC) (Equation 2)
Where XC is capacitive reactance (in ohms) and C is capacitance (in farads).
Note that capacitive reactance is inversely proportional to frequency. Therefore, as frequency increases, capacitive reactance decreases. You should also note that capacitive reactance will cause current to lead voltage by 90 degrees.
Conductor geometry
The inductance and, as a result, the inductive reactance of a cable is a function of its geometry and physical relationship to other cables. Most engineers and cable manufacturers use very complex series of equations to calculate the inductive reactance of cables. However, you can use the following simplified equation:
XL = 2ϖf × [ (0.1404 × log10 (S ÷ r)) + 0.0153 ] × 10-3 (Equation 3)
Where XL is inductive reactance (in ohms per 100 feet to neutral), f is frequency (in Hertz), S is the center-to-center distance between single conductor cables (in inches), and r is the radius of the single conductor cable (in inches).
You can use the following equation as well:
XL = .023 × [(loge 2 × (S ÷ d)) + K ] (Equation 4)
Where d is the diameter of the single conductor (in inches) and K is equal to 0.25 for cable with Class B stranding.
You can apply either Equation 3 or 4 to cables with open-circuited sheaths and to single-conductor cables in random lay within raceways.
To make things easier for you, manufacturers provide reactance calculation nomographs that permit the determination of reactances per insulation thickness and conductor size for conductors at various spacings, a sample of which is shown in the Figure (click here to see Figure).
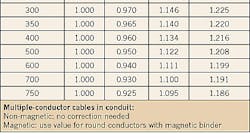
(A nomograph is a graphical calculating device and a two-dimensional diagram designed to allow the approximate graphical computation of a function. It typically has three scales: two scales represent known values and one is the scale where the result is read off. The known scales are placed on the outside (i.e., the result scale is in the center). Each known value of the calculation is marked on the outer scales, and a line is drawn between each mark. Where the line and the inside scale intersect is the result. These reactance values are derived from Equation 3. Based on the conductor and/or cable construction, you must apply the correction factors shown in the Table to any reactance values you obtain.
Because the resultant reactance values are in ohms to neutral, you need to take an additional step to find the phase-to-phase reactance. For a 3-phase system, the phase-to-phase reactance is equal to 1.732 times the phase-to-neutral value. For a single-phase system, the total reactance is twice the phase-to-neutral reactance.
Sample inductive reactance problems
Problem 1. Suppose you have a 3-conductor, 500kcmil, 600V cable with galvanized interlocked armor on a 3-phase, 3-wire, 60Hz feeder circuit. Each conductor has 65 mils of insulation. What is the cable's phase-to-phase reactance?
Because you have 600V singles within the 3-conductor cable, each individual single conductor has no separation tapes, semicon tapes, shields, or other coverings. As such, you can refer to reactance tables and directly use the reactance value indicated in the “65 mil” column for 500kcmil, which is 0.0251 ohms per 1,000 feet to neutral.
Because the multiconductor cable's steel interlocked armor is similar to a magnetic binder, however, you have to multiply this value by the appropriate correction factor shown in the Table, which in this case is 1.122. So, XL is equal to 0.0251 times 1.122, or 0.0282 ohms per 1,000 feet to neutral.
The phase-to-phase reactance for this circuit is equal to 0.0282 times 1.732, or 0.0488 ohms per 1,000 feet.
Problem 2. Suppose you have a 15kV feeder consisting of three, random lay, 350kcmil, 100% insulation level, single conductors, each with concentric wire strand shields, in a galvanized steel conduit. Each conductor has an O.D. of 1.34 in.
Because the 15kV construction includes a separation tape, a semicon tape, concentric wire stranding, and a jacket, you cannot just use the insulation thickness typically noted for 100% insulation level, which is normally 175 mils. To be more accurate, you need to calculate insulation thickness by using the following equation:
Thickness = [(single-conductor O.D. 2 bare wire O.D.) ÷ 2]
Now, you know the conductor O.D. is 1.34 inches. From wire and cable literature, you can find that a 37-strand, Class B, 350kcmil bare conductor has a nominal O.D. of 0.681 inches. So, the insulation thickness is the quantity 1.34 inches minus 0.681 inches divided by 2, or 0.33 inches (330 mils). Per the reactance tables, the reactance value is 0.0373.
Because the conductors are in a magnetic conduit, you must multiply this value by 1.50 (increase of 50%). Therefore, the inductive reactance-to-neutral at 6-Hz in ohms per 100 feet (XL) is equal to 0.0373 times 1.50, or 0.0560. The phase-to-phase reactance is 0.0560 times 1.732, or 0.097 ohms per 1,000 feet.
Next month, we'll talk about how to calculate inductive reactance in instances where cables are not touching but are in specific geometric configurations.