When you determine conductor sizes for low-voltage feeder or branch circuits, do you account for voltage drop? Some people believe this is unnecessary, and some believe that doing so is a Code requirement. The first belief is false, but the second is only partly true.
For sensitive electronic equipment, branch circuits can't have more than a 1.5% voltage drop, and the combined voltage drop of feeder and branch-circuit conductors can't exceed 2.5% [647.4(D)]. For all other circuits, the 2005 NEC merely recommends 3% or 5%, depending on the circuit type (feeder or branch) and load type [210.19(A)(1) FPN No. 4 and 215.2(A)(3) FPN No. 2]. Engineering and design standards, coupled with specific user requirements, determine the allowable voltage drop for feeders and branch circuits.
Equipment manufacturers typically recommend or require a minimum circuit voltage or percentage of the equipment voltage rating. For example, one manufacturer may state that voltage at the device must be between 466V and 494V. Another may require that the voltage drop not exceed 3% of the nameplate voltage.
Low voltage on a system increases maintenance costs and decreases safety and performance. Operating electrical equipment below its acceptable voltage rating can lead to premature failure and hazardous situations. Inductive loads, such as motors and ballasts can overheat, shortening equipment life and increasing energy consumption. If operated below their rated voltage, resistive loads, such as heaters, simply won't provide the desired output. A 10% reduction of voltage reduces the power output by 19%, because power output reduces as the square of voltage. Reduced circuit voltage can cause lights to flicker when other appliances or equipment cycle on.
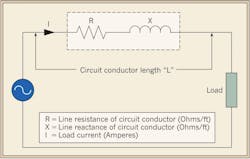
Sizing the circuit conductor. To correctly determine the minimum conductor size for a given ampacity, you first must determine the voltage drop for that circuit. You can do this by one of several methods. For example, you can calculate the voltage drop of the simple two-wire AC circuit in the Figure by using the following equation,
where Vd is voltage drop, K is the resistivity constant of conductor metal (circular mil-ohm per foot), Q is the alternating current adjustment factor for skin effect, L is the length of circuit (in feet), I is the load (current draw in amps), and CM is the cross sectional area of conductor (in circular mils). CM may also be denoted as D.
For a single-phase AC circuit, when only one-way conductor length needs to be considered (as in a balanced, 3-phase, 4-wire circuit with zero current flowing through the neutral), the voltage drop is half of the drop calculated by the preceding equation. For a balanced 3-phase, 3-wire circuit, the voltage drop between any two phase conductors is 0.866 times the voltage drop calculated by the preceding equation.
Notice that the calculation requires you to determine some facts about ambient condition and the load, wire/cable, and raceway characteristics.
If you find the calculations tedious, you can refer to the voltage drop tables often found in handbooks and design guides; the values obtained are usually sufficient for design purposes. Software can also provide an efficient means of calculating voltage drop.
If you use the previous equation as is, you can plug in the values on the right side of the equation and determine the voltage drop on the left side as the result. If the answer you get is too high, you could try changing the conductor to the next higher size and try the equation again. If your answer is still too high, you can keep increasing the conductor size until your calculated voltage drop is acceptable. However, this method can quickly become tiresome — especially on a large project.
A more efficient approach is to first determine what voltage drop is acceptable. Then use a form of the equation that lets you determine the required conductor size. For example, if you know that your maximum voltage drop is going to be 14V (3% of 480V), you can determine the conductor size with the following equation, which is a reworked version of the first equation.
Circuit parameters. Regardless of how you determine voltage drop, you must always know certain things about the circuit in question. These are called “circuit parameters.” Getting these circuit parameters correct will require some evaluation and perhaps some fact digging.
What do these parameters include? While you need to account for some factors to adjust for accuracy, you need to know conductor resistivity and length, plus the current draw just to “do the math” of the equations.
Conductor resistivity. Conductor resistance increases with temperature. Hence, the resistivity constant employed in the calculation should be the value corresponding to the operating temperature of the conductors. The resistivity constant for copper conductor voltage drop calculations is 12.9 ohms at 90°C and 10.8 ohms at 60°C. The resistivity constant for aluminum is 21.2 ohms at 90°C and 17 ohms at 60°C.
Adjustment for skin effect. For small wires, up to 3 AWG, resistance is the same for 60 Hz AC and DC. But above 3 AWG, AC resistance is larger due to skin effect, which causes the current to flow through the periphery of the conductor, thus reducing its effective cross sectional area. The adjustment factor for skin effect is derived by taking AC resistance value and dividing it by DC resistance value. The DC and AC resistance values can be obtained from NEC Chapter 9 Tables 8 and 9.
Consider the following example. For a 4/0 AWG copper conductor:
DC resistance=0.0608 ohms/1,000 ft for uncoated conductor (Table 8)
AC resistance=0.063 ohms/1,000 ft for uncoated conductor in steel conduit (Table 9)
This means that the AC resistance is 1.0362 times the DC resistance.
Circuit conductor length. The length of the circuit conductor is simply the distance from source to the load. But is it the closest load, the farthest load, or some load in the middle? The answer is none of the above.
Using the entire length of circuit conductor to the farthest load means you'll calculate erroneously high voltage drop values and thus may needlessly oversize the circuit conductors. The rules of series-parallel circuits come into play here. When a feeder (or branch conductor) reaches the first load, it's carrying the full current. But it doesn't carry the full current to each subsequent load; current divides proportionate to the impedance of each load. This reveals the following two facts:
-
If you use the length of the circuit to the closest load, you neglect to account for that part of the circuit past the first load. The calculated voltage drop would be less than the actual.
-
If you use the actual length of the circuit — from source to the farthest load — the calculated voltage drop would be greater than the actual.
You need to determine what conductor length would be equivalent to having all loads concentrated at one point — the “load nexus” of the circuit. In the simplest of situations, in which the loads are equal and spaced evenly along the circuit, the load nexus is obviously halfway between the first and last load. If the loads are unequal and/or spaced unequally, you'll need to apply series-parallel calculations to accurately determine where the load nexus is. However, these calculations are beyond the scope of this article.
Circuit current. Use the expected steady-state load demand current to calculate the voltage drop. But don't just add up all the loads and call that your total load. Determine the total load by considering the maximum load occurring at any time due to simultaneous operation. Use this demand load for calculating the voltage drop. You may need to allow for future demand as well. If you size your conductors to just barely accommodate the present load, adding load later is going to be expensive. It's much less costly to install slightly oversized wire now than to rip it out and install a new conductor later. Pay special attention to lighting and appliance circuits and to mains that feed several loads.
Load power factor. You should adjust the expected circuit current to account for power factor (PF). How do you determine the PF of loads when one feeder supplies several loads? It's a three-step process:
-
Multiply the kVA of each load by its operating PF.
-
Add these products for all loads.
-
Divide the sum obtained by the total kVA connected to the circuit.
Though approximate, this method allows you to adequately adjust for PF.
Reactance. Chapter 3 wiring methods address the issue of reactance by requiring you to run all three phase conductors of a given circuit in the same raceway if you use ferrous raceways [300.3(B)]. If you use nonferrous raceways, you can use an “isolated phase” arrangement [300.3(B)(1) Ex]. If your installation doesn't follow these requirements, all bets are off.
You can see that you may have to do more than simply plug in whatever numbers you have on hand if you want to perform accurate voltage drop calculations. The accuracy of these calculations will determine how accurately you size your circuit conductors.
Correctly sizing your circuit conductors allows you to provide the most cost-effective installation and the most efficient operation. But incorrect estimations may cause you to oversize or undersize your circuit conductors.
Oversizing the circuit conductors leads to additional cost in terms of raceways, supports, fittings, enclosures, and installation labor. Undersizing leads to operating inefficiencies, overheating, and premature equipment failure. If you correctly determine the voltage drop calculation parameters — especially conductor length — before making the calculation, you'll avoid both of these problems.
Pandian is a project manager with A. Al-Saihati, A. Fattani & O. Al-Othman Consulting Engineering Co. (SOFCON) in Al-Khobar, Saudi Arabia.